Topic : Average PYQ

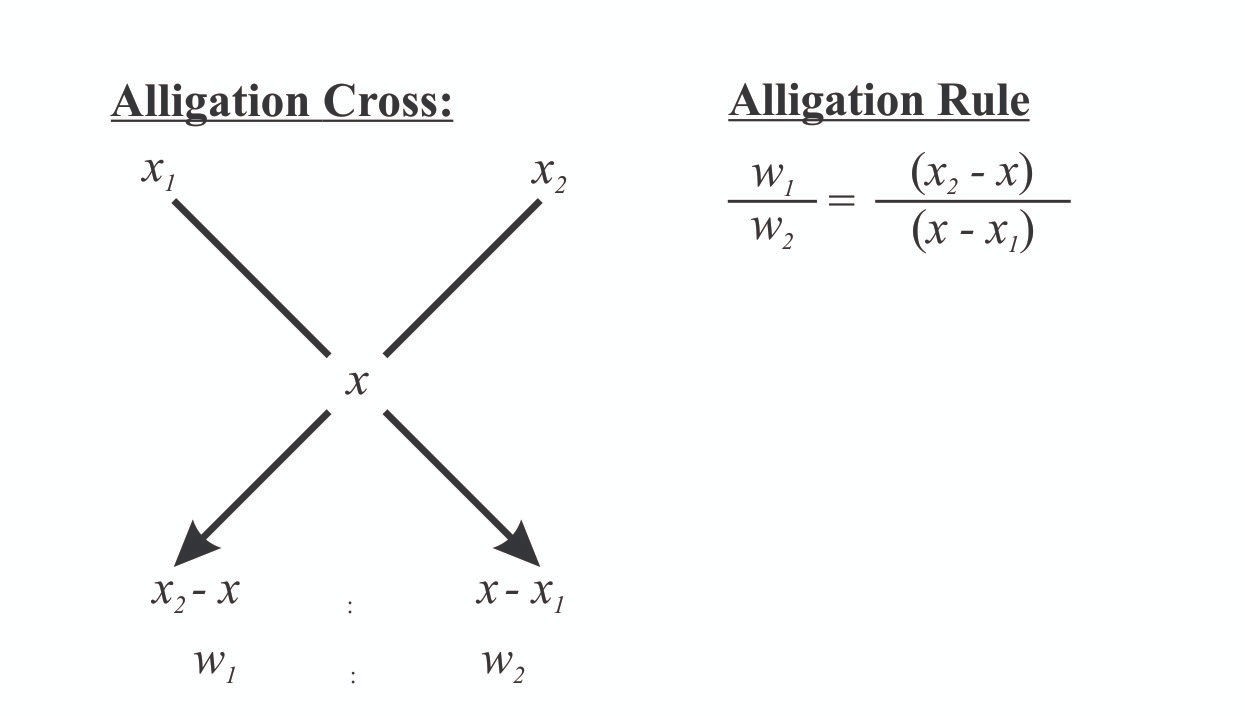
FORMULAE OF AVERAGE

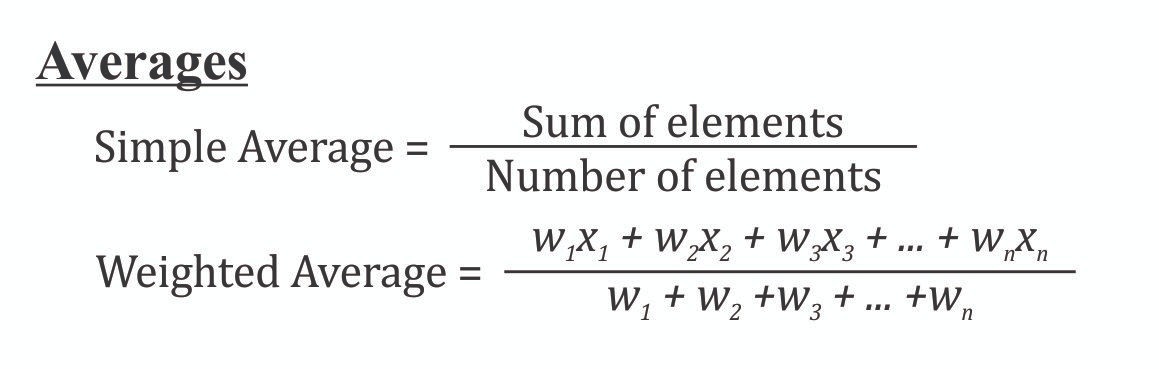
Q1. A student on her first 3 tests received an average score of N points. If she exceeds her previous average score by 20 points on her fourth test, then what is the average score for the first 4 tests? [CSAT 2011]

(a) N + 20

(b) N + 10

(d) N+5

Solution:

Given that,

A student on her first 3 tests received an average score of N points.

First test = N

Similarly, second and third test = N + N = 2N

Fourth test = N + 20

Total score for 4 test = 3N+N+20 = 4N+20

Average = (4N + 20) /4 = N + 5

Hence option (d) is correct

Q2. A group of 630 children is seated in rows for a group photo session. Each row contains three less children then the row in front of it. Which one of the following number of rows is not possible? [CSAT 2014]

(a) 3

(b) 4

(d) 6

Solution:

Given that,

A group of 630 children is seated in rows for a group photo session.

Total children seated = 630

Each row contains three less children then the row in front of it.

Let A be the number of children in 1^st row

Case I: If there are three rows

A, A - 3 and A - 6

A + A - 3 + A - 6 = 630 = 3A - 9 = 630 or A = 213

Thus it is possible

Case II: 4 rows

A + A - 3 + A - 6 + A - 9 = 630 or A = 162 which is possible

Case III: 5 rows

A + A - 3 + A - 6 + A - 9 + A - 12 = 630 or A = 132 which is possible

Case IV: 6 rows

A + A - 3 + A - 6 + A - 9 + A - 12 + A - 15 = 630 or A = 112.5 (NOT POSSIBLE)

Hence option (d) is correct

Q3. The sum of the ages of 5 members comprising a family, 3 years ago was 80 years. The average age of the family today is the same as it was 3 years ago, because of an addition of a baby during the intervening period. How old is the baby?

[CSAT 2016]

(a) 6 months

(b) 1 year

(d) 2 years and 6 months

Solution:

Given that,

The sum of the ages of 5 members comprising a family, 3 years ago was 80 years.

Average age of the family is same as it was 3 years ago the member increases to 6.

Sum of the Present age of 5 members = 80 + 3 x 5 = 95

3 years ago the sum of ages = 80

Average age of person = 80/5 = 16 years

Average age of 5 person 3 years ago is equal to the average age of 6 person presently

16 x 6 = 96 years

Baby age = 96 - 95 = 1 year

Hence option (b) is correct

Q4. The average monthly income of a person in a certain family of 5 is Rs. 10,000. What will be the average monthly income of a person in the same family if the income of one person increased by Rs. 1,20,000 per year? [CSAT 2016]

(a) Rs. 12,000

(b) Rs. 16,000

(d) Rs. 34,000

Solution:

Given that,

Monthly income of a person in the family of 5 is Rs.10000

Total amount (Monthly income of family) = Rs. 50000

if the income of one person increased by Rs. 1,20,000 per year = 120000/12 = Rs.10000 per month

Monthly income of family increases by = Rs 50000 + Rs.10000 = Rs. 60000

Average monthly income per person = 60000/5 = Rs.12000

Hence option (a) is correct

Q5. Suppose the average weight of 9 persons is 50 kg. The average weight of the first 5 persons is 45 kg, whereas the average weight of the last 5 persons is 55 kg. Then the weight of the 5th person will be [CSAT 2017]

(a) 45 kg

(b) 47.5 kg

(d) 52.5 kg

Solution:

Given that,

Average weight of 9 person = 50 kg

Sum of total weight of 9 person = 450 kg

Total weight of first five person = 5 x 45 = 225 kgs

Total weight of last five person = 5 x 55 = 275 kgs

Total weight of first five and last five persons = 275 + 225 = 500 kg

Weight of the 5th person = 500 - 450 = 50kg

Hence option (c) is correct

Q6. The average rainfall in a city for the first four days was recorded to be 0.40 inch. The rainfall on the last two days was in the ratio of 4:3. The average of six days was 0.50 inch. What was the rainfall on the fifth day? [CSAT 2017]

(a) 0.60 inch

(b) 0.70 inch

(d) 0.90 inch

Solution:

Given that,

Average rainfall in a city for the first four days = 0.40 inch

The average of six days = 0.50 inch

rainfall on the last two days = 4: 3

Let A, B, C, D, E and F be 6 days rainfall

E and F = 4a and 3a

Now,

(A + B + C + D)/4 = 0.40

A + B + C + D = 4 x 0.40 = 1.6 inch.......(i)

A + B + C + D + E + F = 6 x 0.5 = 3 inch......(ii)

Substituting equation (i) in (ii)

4a + 3a = 3 -1.6

7a = 1.4 or a = 0.2

On fifth day which is E the rainfall = 0.2 x 4 = 0.80 inch

Hence option (c) is correct

Q7. There are thirteen 2-digit consecutive odd numbers. If 39 is the mean of the first five such numbers, then what is the mean of all the thirteen numbers? [CSAT 2017]

(a) 47

(b) 49

(d) 45

Solution:

Given that,

There are thirteen 2-digit consecutive odd numbers

39 is the mean of the first five such numbers

Let the number be 2a + 1, 2a + 3, 2a + 5.........2a +25

Average of first five = 2a + 1 + 2a + 3 + 2a + 5 + 2a + 7 + 2a + 9 =39 x 5

10a + 25 =195

10a = 170

a = 17

Thus the first number = 2a + 1 = 35

Numbers are 35, 37, 39.....59

Sum of terms ,

Sn = n/2 [first term + last term]

Sn = 13/2 [35+59]

= 611

Now the mean of 13 number = (35 + 37 + 39 + 41....+ 59)/13 = 611/13 = 47 (alternatively to find the sum from 35 to 59 use Sum of A.P formula)

Hence option (a) is correct

Q8. A family has two children along with their parents. The average of the weights of the children and their mother is 50 kg. The average of the weights of the children and their father is 52 kg. If the weight of the father is 60 kg, then what is the weight of the mother? [CSAT 2019]

(a) 48 kg

(b) 50 kg

(d) 54 kg

Solution:

Given that,

A family has two children

The average of the weights of the children and their mother = 50kg

The average of the weights of the children and their father = 52 kg

Weight of the father = 60 kg

Now,

The total sum of weight of children and mother = 50 x 3 = 150kgs

The total sum of weight of children and Father = 52 x 3 = 156kgs

Let children be A and B and father and mother be F and M

A + B = 156 - F = 156 - 60 = 96kgs

M = 150 - 96 = 54kgs

Hence option (d) is correct

Q9. The average marks of 100 students are given to be 40. It was found later that marks of one student were 53 which were misread as 83. The corrected mean marks are [CSAT 2019]

(a) 39

(b) 39.7

(d) 40.3

Solution:

Given that,

The average marks of 100 students = 40

Total marks = 4000

Misread marks difference = 83 - 53 = 30 marks

Now the total corrected marks = 4000 - 30 = 3970

Corrected total average marks = 3970/100 = 39.7

Hence option (b) is correct

Q10. In a class, there are three groups A, B and C. If one student from group A and two students from group B are shifted to group C, then what happens to the average weight of the students of the class? [CSAT 2020]

(a) It increases.

(b) It decreases.

(d) No conclusion can be drawn due to insufficient data.

Solution:

Given that,

Groups are A, B and C in a class

One student from group A and two students from group B are shifted to group C

Now,

Total average weight of the class remains the same as none of the students went out of the class and the groups are within the class.

Hence option (c) is correct

Q11. The average age of a teacher and three students is 20 years. If all the three students are of same age and the difference between the age of the teacher and each student is 20 years, then what is the age of the teacher? [CSAT 2020]

(a) 25 years

(b) 30 years

(d) 45 years

Solution:

Given that,

The average age of a teacher and three students = 20 years

Let the age of students be S

All the three students are of same age = 3S

The difference between the age of the teacher and each student is 20 years

Total age of teacher and three students = 4 x 20 = 80

Let the age of teacher be T

3S + T = 80....(i)

T - S = 20.....(ii) According to question

80 - 3S - S = 20 (Substituting equation (i) in (ii)

60 = 4S

S = 15 years

Thus T = 20 + 15 = 35 years

Hence option (c) is correct

Q12. The average score of a batsman after his 50th innings was 46.4. After 60th innings, his average score increases by 2.6. What was his average score in the last ten innings? [CSAT 2020]

(a) 122

(b) 91

(d) 49

Solution:

Given that,

The average score of a batsman after his 50th innings = 46.4

Average score increases after 60th inning = 2.6

So average score after 60th inning = 46.4 + 2.6 = 49

Total score of 50 innings = 50 x 46.4 = 2320

Total score of 60 innings = 60 x 49 = 2940

Total score of last 10 innings = 2940 - 2320 = 620

Total average score of last 10 innings = 620/10 = 62

Hence option (c) is correct

Q13. There are two Classes A and B having 25 and 30 students respectively. In Class-A the highest score is 21 and lowest score is 17. In Class-B the highest score is 30 and lowest score is 22. Four students are shifted from Class-A to Class-B.

Consider the following statements: [CSAT 2021]

1. The average score of Class-B will definitely decrease.

2. The average score of Class-A will definitely increase. Which of the above statements is/are correct?

(a) 1 only

(b) 2 only

(d) Neither 1 nor 2

Solution:

Given that,

Class A = 25 students

Class B = 30 students

Class A highest score and lowest score = 21 and 17

Class B highest score and lowest score = 30 and 22

Four students shifted from Class A to B

Total students in Class A = 25 - 4 = 21 students

Total students in Class B = 30 + 4 = 34 students

Now,

Statement 1: The average score of Class-B will definitely decrease.

Yes. The average score of Class B will definitely decrease as the highest score of class A is not even the lowest score of Class B. Thus students from class A shifting to class B will definitely decrease the score.

Statement 2: The average score of Class-A will definitely increase.

This cannot be predicted as it will purely depend on scores.

Hence option (a) is correct

Q14. The average weight of A, B, C is 40 kg, the average weight of B, D, E is 42 kg and the weight of F is equal to that of B. What is the average weight of A, B, C, D, E and F? [CSAT 2022]

(a) 40.5 kg

(b) 40.8 kg

(d) Cannot be determined as data is inadequate

Solution:

Given that,

The average weight of A, B, C = 40 kg

the average weight of B, D, E = 42 kg

F = B

A + B + C = 40 x 3 = 120

B + D + E = 42 x 3 = 126 (as B = F) or F + D + E = 126

Average weight of (A + B + C + D + E + F)/6 = (120 + 126)/6 = 41kgs

Hence option (c) is correct

Q15. For five children with a

Question: What is the age of the youngest child?

Statement-1: The age of the eldest is 3 times the youngest.

Statement-2: The average age of the children is 8 years.

Which one of the following is correct in respect of the above Question and the Statements? [CSAT 2023]

(a) The Question can be answered by using one of the Statements alone, but cannot be answered using the other Statement alone.

(b) The Question can be answered by using either Statement alone.

(c) The Question can be answered by using both the Statements together, but cannot be answered using either Statement alone.

(d) The Question cannot be answered even by using both the Statements together.

Solution:

Given that,

For five children with ages a

Let the ages be

b = a + 2, c = a + 4, d = a + 6, e = a + 8

From statement 1: The age of the eldest is 3 times the youngest.

e = 3a

2a = 8 or a = 4

Thus the ages are 4, 6, 8, 10 and 12

Hence statement 1 alone is sufficient to answer the question

Statement-2: The average age of the children is 8 years.

a + a + 2 + a + 4 + a + 6 + a + 8 = 40

5a + 20 = 40 or a = 4

Thus the ages are 4, 6, 8, 10 and 12

Hence statement 2 alone is sufficient to answer the question

Q16. A Question is given followed by two Statements 1 and II. Consider the Question and the Statements.

Question: If the average marks in a class are 60, then what is the number of students in the class?

Statement-1: The highest marks in the class are 70 and the lowest marks are 50. Statement-II: Exclusion of highest and lowest marks from the class does not change the average.

Which one of the following is correct in respect of the above Question and the Statements? [CSAT 2024]

(a) The Question can be answered by using one of the Statements alone, but cannot be answered using the other Statement alone

(b) The Question can be answered by using either Statement alone

(c) The Question can be answered by using both the Statements together, but cannot be answered using either Statement alone

(d) The Question cannot be answered even by using both the Statements together

Solution:

Given that,

The average marks of class is 60

Statement I: The highest marks in the class are 70 and lowest marks are 50.

Statement II: Exclusion of highest and lowest marks from the class does not change the average.

Now,

Let the number of students be S and total marks obtained M

60 = M/S

M = 60S

From Statement I: The highest marks in the class are 70 and lowest marks are 50.

From the highest and the lowest marks the number of students cannot be determined

Hence statement I is insufficient to answer the question

From Statement II: Exclusion of highest and lowest marks from the class does not change the average.

(M - 70 - 50)/(S - 2) = 60

(M - 70 - 50) = 60S - 120

M = 60S

Hence statement II is insufficient to answer the question

Also,

Combining both the statements:

There is no sufficient data to answer the question

Hence option (d) is correct

Q17. Consider the following:

Weight of 6 boys = Weight of 3 men = Weight of 7 girls = Weight of 4 women

If the average weight of the women is 63 kg, then what is the average weight of the boys? [CSAT 2024]

(a) 40 kg

(b) 42 kg

(d) 63 kg

Solution:

Given that,

Weight of 6 boys = Weight of 7 girls = Weight of 3 men = Weight of 4 women

Average weight of women = 63kg

Now,

Let boys B, Girls be G, Men be M and Women be W

6B = 7G = 3M = 4W

Let K be the Constant

B = K/6, G = K/7, M = K/3 and W = K/4

Ratio = (K/6) : (K/7) : (K/3) : (K/4)

LCM of (3, 4, 6, 7) = 84

Total ratio = 14K : 12K : 28K : 21K

Average weight of women = 63kg

So, 63/21 = 3

Thus, K = 3

Therefore the average weight of boys = 14 x 3 = 42kg

Hence option (b) is correct

ANSWER KEY

1. D

2. D

3. B

4. A

5. C

6. C

7. A

8. D

9. B

10. C

11. C

12. C

13. A

14. C

15. B

16. D

17. B

Average PYQ

Topic : Average PYQ

Related Links:

Enquiry Now

Enquiry Now